Many applications require automated clustering and dynamic stream into groups which are based on their similarities.
For example: Analyzing web click streams, stock market analysis, network intrusion, etc.
New methodologies for clustering are:
1. Divide and conquer method:
This method sequentially divides data streams into chunks on the basis of their arrival. Then, the summary of these chunks are computed and merged, which assist in constructing the larger model through the smaller blocks.
2. Computation of previous data and storing its summary:
The limited memory and requirement of fast response summary of previously known data is computed and stored. Such summaries are used to compute the important statistics.
3. Exploring multiple time granularity to analyze the cluster evolutions:
This technique uses a tilted time frame model to store snapshots of summary of data at different time frames.
4. Dividing stream clustering into off-line and on-line processes:
In this method, the summary of data is computed, stored and incrementally updated.
Dynamic clusters are maintained through on-line process. The off-line process can be used if the user has queries about previous or current cluster.
Graph Based Database and Graph Mining
- Graphs can be used in modeling of various applications and their interactions.
For example: Bioinformatics, web analysis, computer vision, chemical informatics etc. - Frequent subgraph patterns can be mined for further classification and clustering of important tasks.
- Frequent substructure are the basic patterns to be discovered in the collection of graph. Substructures can be used to characterize and find the different graphs within the graph.
- Graph mining methods and algorithms are widely studied in various applications to discover the interesting patterns.
Example: Active chemical structures in HIV screening datasets can be designed using graph mining of frequent graphs between the different classes.
Methods for mining frequent subgraphs
Before learning the methods for mining frequent subgraph, let's learn about the some basic terms of frequent subgraph:
V (g): Represents the vertex set of graph 'g'.
E (g): Represents the set of edges.
L: It is a label function to map a vertex.
g: A graph which is subgraph of another graph g',if there exists a subgraph isomorphism from g to g'.
D: Given labeled dataset as, D = {G1, G2, G3}
Suppose (g) is the number of percentage of graphs in D, where g is a subgraph. A frequent graph is a graph whose support value is not less than minimum support threshold min
_sub.
Example: Demonstration of frequent subgraph.
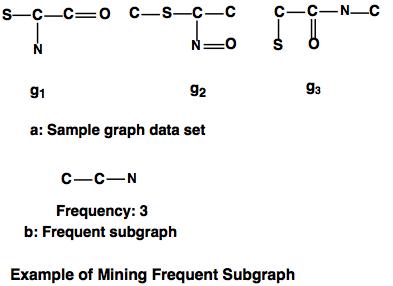
In this example, the sample graph data sets are given as g1, g2, g3 and the frequent subgraph is derived with frequency 3.
Approaches for frequent substructure mining
1. Apriori based approach
Apriori uses a bottom-up approach. The search starts with graphs of small size and generation of candidates by including an extra vertex or edge or path.
The Apriori Graph algorithm for substructure mining can be explained as
- Let Sk be the frequent substructure set of size k. In Apriori algorithm, after each iteration, size of new (discovered) frequent substructure is incremented by one.
- These new substructures can be generated by joining two slightly different frequent subgraphs, which is regarded as Apriori Graph. Then, next step is to check out the frequency of new graph.
- Apriori algorithm uses breadth-first-search and Hash tree structure to count candidate item sets of length k from item sets of length ( k-1). This newly created candidate includes (k-1) size subgraph and additional 2 vertices from the two size-k patterns.
Example:
Consider the following database, where each row is transaction and each cell is an individual item of transaction as:
The association rules which can be determined from this database are stated as:- 100 % of sets with A with contain B
- 50% of sets with A and B have E
- 50% of sets with A and B have T
2. Pattern growth approach- In this approach, BFS ( Breadth First Search) and DFS (Depth First Search) mechanisms are used.
- For every (new) discovered graph 'g', recursion process is applicable over all the frequent graphs so as to discover embedded 'g' graphs.
- The recursion process stops when it is not possible to generate the frequent graph.
- If the same graph is discovered multiple times, then it is highly impossible to extend a graph.
Algorithm
1. If g ∈ s, then return to initial position;
2. Else insert g into s;
3. Scan 'D' and determine all the edges 'e' to execute 'g' in the form of 'g
◊x e' ;
4. Perform recursion for each frequent g
◊x e;
5. Pattern growth graph (g
◊x e; D, min-sup s);
6. Return.
