Associations in Data Mining

Market Basket Analysis

• It is a modeling technique that helps to identify which items should be purchased together.
• Assume that, there are large number of items  like “Tea”, “Coffee”, “Milk” “Sugar”. Among these, the customer buys the subset of items as per the requirement and market gets the information of items which customer has purchased together. So, the market uses this information to put the items on different positions (or locations).

Implementation of market based analysis

• The market basket analysis is used to decide the perfect location, where the items can be placed inside the store.
  For example: If the customer buys a coffee, it is possible that the customer may buy milk or sugar along with coffee.
• So keeping the coffee and sugar next to each other in store will be helpful to customers to buy the items together and improves sales of the company.
• The problem of large volume transactions can be minimized by using differential market basket analysis, which is capable of finding interesting results and eliminates the large volume.

Frequent Item-sets, Closed item-sets and Association Rules

Frequent Item-sets

• Frequent item-sets are used in association rules.
• An itemset is said to be frequent, if X's support is no less than a minimum support threshold.
• A frequent item-set is a set of items that may appear at least in pre- defined number of transactions.

Steps to find frequent item-sets:
1. A level wise search can be carried out to find the frequent-1 items (set of size 1), then proceed to find frequent- 2 items and so on.
2.  All maximum frequent item-sets are searched in this step.

Closed Item-sets

• Consider two item-sets 'X' and 'Y', if each item of 'X' is in 'Y', but there is at least one item of 'Y', that is not in 'X' then 'Y' is not a proper super-item set of 'X'. In this case item set is closed.
• If 'X' is closed and frequent, then it is called as closed frequent item-set.

Association Rules

• The objects or items from relational databases, transactional databases or other information repositories are considered to find frequent patterns, associations and correlations.
• Association rules search for interesting relationships among the items in a given data set by examining transactions.
  For example - Frequently purchased item- sets can be easily found out by examining the shop cart. This helps in advertising or for placement of goods in the store.
• Association rules have general form:
  I₁  →  (where I₁ ∩ I₂ = 0)
• The rule can be read as, Given that someone has purchased the items from the set I₁, then they are likely to also buy the items in the set I₂.

Large Item-sets

• It is a set of single items, from transactions.
• If some items occur together, then they can form an association rule.

Support:

• It is the percentage of the transactions in which the items appear.
• If A => B
• Support (A → B) =  # _ tuples containing both A and B / total #_tuples
• The support for an association X => Y is the percentage of transactions in the database that contains X U Y.

Confidence:

• The confidence or strength for an association rule A => B is the ratio of the number of transactions that contain A.
• Consider a rule A => B, which is a measure of ratio of the number of tuples containing both A and B to the number of tuples containing 'A'.

Confidence (A → B) = #_tuples containing both A and B / #_tuples_containing A

Solved example of apriori algorithm

Example: Find the frequent item sets in the given table, with minimum support of 50% and confidence 50%.

TID	List of items
T2000	A, B, C
T1000	A, C
T4000	A, D
T5000	B, E, F

Solution:
Step 1: Scan D for count each candidate. The candidate list is {A, B, C, D, E, F}
C₁ =        

Items	Support
{A}	3
{B}	2
{C}	2
{D}	1
{E}	1
{F}	1

Step 2: Compare the candidate support with minimum support count (50%)
L₁ =

Items	Support
{A}	3
{B}	2
{C}	2

Step 3: Generate candidate C₂ from L1
C₂  =

Items
{A, B}
{A, C}
{B, C}

          
Step 4: Scan D for count of each candidate in C₂ and find the support.
C₂ =    

Items	Support
{A, B}	1
{A, C}	2
{B, C}	1

Step 5: Compare candidate (C₂) support count with the minimum support count.
L₂  =

Items	Support
{A,C}	2

Step 6:  
Data contains the frequent item 1 (A, C), so that the association rule that can be generated from 'L' are as shown in the following table with the support and confidence.

Association Rule	Support	Confidence	Confidence %
A - > C	2	2/3 = 0.66	66 %
C - > A	2	2/2 = 1	100 %

So the final rules are:
Rule 1: A - > C
Rule 2: C - > A

FP- Growth Algorithm by Jiawei Han et al.

• This algorithm allows to find frequent item-set without generation of candidate item-set.
• Once the F- P tree is generated, it is mined by calling FP_growth (FP_tree, null).
  Procedure FP_ growth (Tree, α):
• If tree consist of a single path 'P', then for each combination (which is denoted as 'β' ) of the path 'P' generates the pattern β U , α with support count = of nodes in β;
• Else, for each a_i in the header of tree, generates the patterns  β = a_i.support_count;
• So, construct β's conditional pattern base first and then β's conditional FP _Tree Treeβ;
• If Tree β ≠ Ф
• Then, call FP_ growth (Treeβ, β); }

Example:
Given transaction database, find the frequent patterns with min support = 2.

TID	List of item
T1	A1, A2, A5
T2	A2, A4
T3	A2, A3
T4	A1, A2, A4
T5	A1, A3
T6	A2, A3
T7	A1, A3
T8	A1, A2, A3, A5
T9	A1, A2, A3

Item	Support
A1	6
A2	7
A3	6
A4	2
A5	2

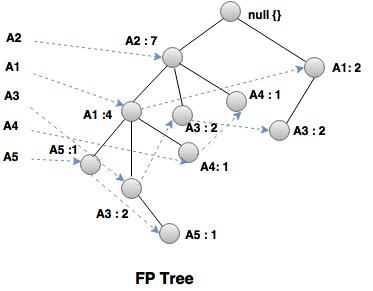
Item	Conditional pattern base	Conditional FP-tree	Frequent patterns generation
A5	{(A2 A1: 1)}	{ A2: 2, A1: 2}	A2 A5: 2, A1 A5: 2, A2 A1A5: 2
A4	{A2 A1 : 1), (A2:1)}	{A2: 2}	A2 A4: 2
A3	{( A2, A1 :2), (A1: 2)}	(A2: 4, A1:2), (A1:2)	A2 A3: 4, A1, A3: 2, A2 A1A3: 2
A1	{(A2: 4)}	{(A2: 4)}	A2 A1: 4