Regression in Data Mining

Regression involves predictor variable (the values which are known) and response variable (values to be predicted).

The two basic types of regression are:

1. Linear regression

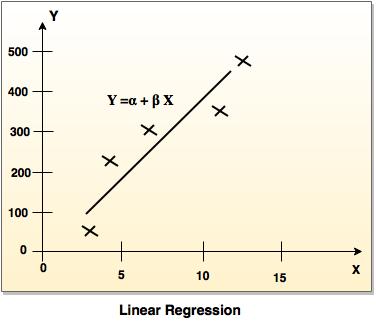
• It is simplest form of regression. Linear regression attempts to model the relationship between two variables by fitting a linear equation to observe the data.
• Linear regression attempts to find the mathematical relationship between variables.
• If outcome is straight line then it is considered as linear model and if it is curved line, then it is a non linear model.
• The relationship between dependent variable is given by straight line and it has only one independent variable.
  Y =  α + Β X
• Model 'Y', is a linear function of 'X'.
• The value of 'Y' increases or decreases in linear manner according to which the value of 'X' also changes.

2. Multiple regression model

• Multiple linear regression is an extension of linear regression analysis.
• It uses two or more independent variables to predict an outcome and a single continuous dependent variable.
  Y = a₀ + a₁ X₁ + a₂ X₂ +.........+a_k X_k +e
  where,
  'Y' is the response variable.
  X₁ + X₂ + X_k are the independent predictors.
  'e' is random error.
  a₀, a₁, a₂, a_k are the regression  coefficients.

Naive Bays Classification Solved example

Bike Damaged example: In the following table attributes are given such as color, type, origin and subject can be yes or no.

Bike No	Color	Type	Origin	Damaged?
10	Blue	Moped	Indian	Yes
20	Blue	Moped	Indian	No
30	Blue	Moped	Indian	Yes
40	Red	Moped	Indian	No
50	Red	Moped	Japanese	Yes
60	Red	Sports	Japanese	No
70	Red	Sports	Japanese	Yes
80	Red	Sports	Indian	No
90	Blue	Sports	Japanese	No
100	Blue	Moped	Japanese	Yes

Solution:
Required formula:
              P (c | x) = P (c | x) P (c) / P (x) In the fields of science, engineering and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's true value.

Where,   
P (c | x) is the posterior of probability.
P (c)  is the prior probability.
P (c | x) is the likelihood.
P (x) is the prior probability.

It is necessary to classify a <Blue, Indian, Sports>, is unseen sample, which is not given in the data set.
So the probability can be computed as:
     
P (Yes) = 5/10
P (No) = 5/10

Color
P(Blue|Yes) = 3/5	P(Blue|No) = 2/5
P(Red|Yes) = 2/5	P(Red|No) = 3/5
Type
P(Sports|Yes) = 1/5	P(Sports|No) = 3/5
P(Moped|Yes) = 4/5	P(Moped|No) = 2/5
Origin
P(Indian|Yes) = 2/5	P(Indian|No) = 3/5
P(Japanese|Yes) = 3/5	P(Japanese|No) = 2/5

So, unseen example X = <Blue, Indian, Sports>

P(X|Yes). P(Yes) = P(Blue|Yes). P(Indian|Yes). P(Sports|Yes). P(Yes)
                             = 3/5*2/5*1/5*5/10 = 0.024

P(X|No). P(No) = P(Blue|No). P(Indian|No). P(Sports|No).P(No)
                           = 2/5*3/5*3/5*5/10 = 0.072

So, 0.072 > 0.024 so example can be classified as NO.