What is Knowledge Representation?
- Artificial intelligence is a system that is concerned with the study of understanding, designing and implementing the ways, associated with knowledge representation to computers.
- In any intelligent system, representing the knowledge is supposed to be an important technique to encode the knowledge.
- The main objective of AI system is to design the programs that provide information to the computer, which can be helpful to interact with humans and solve problems in various fields which require human intelligence.
What is Knowledge?
- Knowledge is an useful term to judge the understanding of an individual on a given subject.
- In intelligent systems, domain is the main focused subject area. So, the system specifically focuses on acquiring the domain knowledge.
Types of knowledge in AI
Depending on the type of functionality, the knowledge in AI is categorized as:
1. Declarative knowledge- The knowledge which is based on concepts, facts and objects, is termed as 'Declarative Knowledge'.
- It provides all the necessary information about the problem in terms of simple statements, either true or false.
2. Procedural knowledge - Procedural knowledge derives the information on the basis of rules, strategies, agendas and procedure.
- It describes how a problem can be solved.
- Procedural knowledge directs the steps on how to perform something.
For example: Computer program.
3. Heuristic knowledge - Heuristic knowledge is based on thumb rule.
- It provides the information based on a thumb rule, which is useful in guiding the reasoning process.
- In this type, the knowledge representation is based on the strategies to solve the problems through the experience of past problems, compiled by an expert. Hence, it is also known as Shallow knowledge.
4. Meta-knowledge- This type gives an idea about the other types of knowledge that are suitable for solving problem.
- Meta-knowledge is helpful in enhancing the efficiency of problem solving through proper reasoning process.
5. Structural knowledge- Structural knowledge is associated with the information based on rules, sets, concepts and relationships.
- It provides the information necessary for developing the knowledge structures and overall mental model of the problem.
Issues in knowledge representation
The main objective of knowledge representation is to draw the conclusions from the knowledge, but there are many issues associated with the use of knowledge representation techniques.
Some of them are listed below:
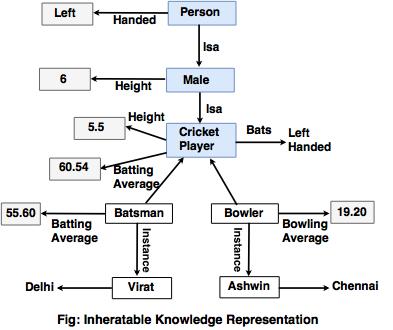 Refer to the above diagram to refer to the following issues.
1. Important attributes
Refer to the above diagram to refer to the following issues.
1. Important attributes
There are two attributes shown in the diagram,
instance and
isa. Since these attributes support property of inheritance, they are of prime importance.
2. Relationships among attributes
Basically, the attributes used to describe objects are nothing but the entities. However, the attributes of an object do not depend on the encoded specific knowledge.
3. Choosing the granularity of representation
While deciding the granularity of representation, it is necessary to know the following:
i. What are the primitives and at what level should the knowledge be represented?
ii. What should be the number (small or large) of low-level primitives or high-level facts?
High-level facts may be insufficient to draw the conclusion while Low-level primitives may require a lot of storage.
For example: Suppose that we are interested in following facts:
John spotted Alex.
Now, this could be represented as "Spotted (agent(John), object (Alex))"
Such a representation can make it easy to answer questions such as: Who spotted Alex?
Suppose we want to know : "Did John see Sue?"
Given only one fact, user cannot discover that answer.
Hence, the user can add other facts, such as "Spotted (x, y) → saw (x, y)"
4. Representing sets of objects.
There are some properties of objects which satisfy the condition of a set together but not as individual;
Example: Consider the assertion made in the sentences:
"There are more sheep than people in Australia", and "English speakers can be found all over the world."
These facts can be described by including an assertion to the sets representing people, sheep, and English.
5. Finding the right structure as needed
To describe a particular situation, it is always important to find the access of right structure. This can be done by selecting an initial structure and then revising the choice.
While selecting and reversing the right structure, it is necessary to solve following problem statements.
They include the process on how to:
- Select an initial appropriate structure.
- Fill the necessary details from the current situations.
- Determine a better structure if the initially selected structure is not appropriate to fulfill other conditions.
- Find the solution if none of the available structures is appropriate.
- Create and remember a new structure for the given condition.
- There is no specific way to solve these problems, but some of the effective knowledge representation techniques have the potential to solve them.
Logic Representation
Facts are the general statements that may be either True or False. Thus, logic can be used to represent such simple facts.
To build a Logic-based representation:
- User has to define a set of primitive symbols along with the required semantics.
- The symbols are assigned together to define legal sentences in the language for representing TRUE facts.
- New logical statements are formed from the existing ones. The statements which can be either TRUE or false but not both , are called propositions. A declarative sentence expresses a statement with a proposition as content;
Example: The declarative "Cotton is white" expresses that Cotton is white. So, the sentence "Cotton is white" is a true statement.
What is Propositional Logic (PL)?
- Propositional logic is a study of propositions.
- Each proposition has either a true or a false value but not both at a time.
- Propositions is represented by variables.
For example: Symbols 'p' and 'q' can be used to represent propositions.
There are two types of propositions:
1. Simple Preposition
2. compound Prepositions.
1. A simple preposition: It does not contain any other preposition.
For example: Rocky is a dog.
2. A compound preposition: It contains more than one prepositions.
For example: Surendra is a boy and he likes chocolate.
Connectives and the truth tables of compound prepositions are given below:
Consider 'p' and 'q' are two prepositions then,
1. Negation (¬p) indicates the opposite of p.
Truth table for negation:
2. Conjunction (p ∧ q) indicates that p and q both and are enclosed in parenthesis. So, p and q are called conjuncts .
Truth table for conjunction:
3. Disjunction (p ∨ q) indicates that either p or q or both are enclosed in parenthesis. Thus, p and q are called disjuncts.
Truth table for disjunction:
4. Implication (p ⇒ q) consists of a pair of sentences separated by the ⇒ operator and enclosed in parentheses. The sentence to the left of the operator is called as an antecedent, and the sentence to the right is called as the consequent.
Truth table for implication:
5. Equivalence (p ⇔ q) is a combination of an implication and a reduction.
Truth table for Equivalence:
