Compound Interest - Aptitude Questions and Answers Part 2

6. Talking to his friend, Raj says, "I invested a certain amount at a compound interest. The amount becomes Rs 900 in 3 years and Rs 1000 if I allow one more years" Find the amount that Raj invested and the rate of interest that he got.

a. Rs. 635.20, 12.50%
b. Rs. 656.10, 11.11%
c. Rs. 696.50, 12.50%
d. Rs. 698.80, 11.11%

Answer: b. Rs. 656.10, 11.11%

Explanation:

If Raj allows, one more year, time period becomes 4 years.
4 years - 3 years = 1 year
Thus, we can say that Rs. 900 becomes Rs. 1000 in 1 year.
∴ Interest = Rs. 1000 - Rs. 900 = Rs. 100
For 1 year time period, Simple Interest = Compound Interest

∴P x R x T=900 x R x 1= Rs. 100
100100
∴ R =100% = 11.11%
9
Also, in 3 years by compound interest the original sum becomes Rs. 900 at the rate 11.11% or100%.
9
∴ Amount = Rs. 900 = P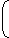1 +R 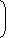n
100
∴ 900 = P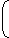1 +100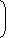3
9 x 100
∴ P = Rs. 656.10


7. A certain sum earns a simple interest of Rs. 400 when invested for 4 years at a rate of 10% per annum. Keeping all the parameters same, what will be the interest earned if the interest offered is compound interest?

a. Rs. 454.50
b. Rs. 464
c. Rs. 464.10
d. Rs. 480.60

Answer: c. Rs. 464.10

Explanation:

Simple Interest =P x R x T= Rs. 400
100
∴P x 10 x 4= 400
100
∴ P = Rs. 1000
For Compound Interest, Amount = P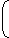1 +R 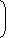n
100
∴ Amount = 1000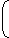1 +10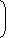4
100
∴ Amount = Rs. 1464.10
∴ Compound Interest = Amount - Principle = Rs. 1464.1 - Rs. 1000 = Rs. 464.10


8. The current population of Town A is 60,000. Increasing at a rate of 10% per annum, what will be the population after 3 years?

a. 75,550
b. 77,250
c. 79,860
d. 80,500

Answer: c. 79,860

Explanation:

Tip:
Population after n years = P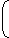1 ±R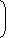n
100
P= Population; R = Rate of increase or decrease; n= number of years;
'+' = during increase; '-'= during decrease


Using formula given above -
Population after 3 years = 60,000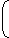1 +10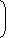3
100
=60,000 x 11 x 11 x 11= 79,860
10 x 10 x 10


9. A money lender lends his money with the condition that the amount should be repaid in 2 yearly installments. The rate of interest will be 20% compounded annually. Find the value of each installment if the amount Raj borrowed was Rs 22,000/-

a. Rs. 11000
b. Rs. 12800
c. Rs. 14400
d. Rs. 16400

Answer: c. Rs. 14400

Explanation:

Tip:
In cases where rate of interest is given and the number of installments = 2, then you should use the following trick to solve such problems quickly.
(1st fraction x 2nd fraction) x Installment = Sum


First express the rate of interest as a fraction.
∴ R = 20% =20=1
1005
Next, derive first fraction as =Denominator=5=5
Numerator+Denominator1+56
Using this fraction, derive 2nd fraction as =Numerator+Denominator=5+6=11
Denominator66
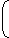∴5x11 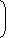x Installment = Sum
66
Here Sum is the borrowed amount
Installment is the value of each installment (including interest on the installment)
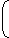∴5x11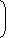x Installment = 22000
66
∴ Installment = Rs. 14400


10. Rohan lends his money to a friend at a rate of 12% per annum. The compound interest accrued at the end of 2 years is Rs 2862/-. Find the amount he lent.

a. Rs. 1220
b. Rs. 10000
c. Rs. 11250
d. Rs. 13500

Answer: c. Rs. 11250

▲