Binary Tree in Data Structure

Binary tree is a special type of data structure. In binary tree, every node can have a maximum of 2 children, which are known as Left child and Right Child. It is a method of placing and locating the records in a database, especially when all the data is known to be in random access memory (RAM).

Definition:

"A tree in which every node can have maximum of two children is called as Binary Tree."

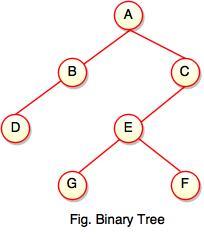
The above tree represents binary tree in which node A has two children B and C. Each children have one child namely D and E respectively.

Representation of Binary Tree using Array

Binary tree using array represents a node which is numbered sequentially level by level from left to right. Even empty nodes are numbered.

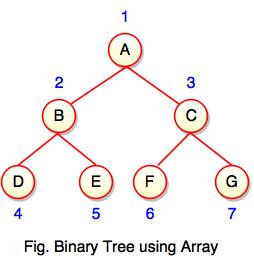
Array index is a value in tree nodes and array value gives to the parent node of that particular index or node. Value of the root node index is always -1 as there is no parent for root. When the data item of the tree is sorted in an array, the number appearing against the node will work as indexes of the node in an array.

location number array tree

Location number of an array is used to store the size of the tree. The first index of an array that is '0', stores the total number of nodes. All nodes are numbered from left to right level by level from top to bottom. In a tree, each node having an index i is put into the array as its i th element.

The above figure shows how a binary tree is represented as an array. Value '7' is the total number of nodes. If any node does not have any of its child, null value is stored at the corresponding index of the array.

Binary Search Tree

Binary search tree is a binary tree which has special property called BST.
BST property is given as follows:

For all nodes A and B,

I. If B belongs to the left subtree of A, the key at B is less than the key at A.

II. If B belongs to the right subtree of A, the key at B is greater than the key at A.

Each node has following attributes:

I. Parent (P), left, right which are pointers to the parent (P), left child and right child respectively.

II. Key defines a key which is stored at the node.

Definition:

"Binary Search Tree is a binary tree where each node contains only smaller values in its left subtree and only larger values in its right subtree."

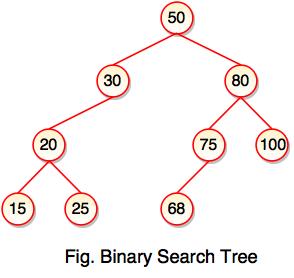
The above tree represents binary search tree (BST) where left subtree of every node contains smaller values and right subtree of every node contains larger value.
Binary Search Tree (BST) is used to enhance the performance of binary tree.
It focuses on the search operation in binary tree.

Note: Every binary search tree is a binary tree, but all the binary trees need not to be binary search trees.

Binary Search Tree Operations

Following are the operations performed on binary search tree:

1. Insert Operation

Insert operation is performed with O(log n) time complexity in a binary search tree.
Insert operation starts from the root node. It is used whenever an element is to be inserted.

The following algorithm shows the insert operation in binary search tree:

Step 1: Create a new node with a value and set its left and right to NULL.

Step 2: Check whether the tree is empty or not.

Step 3: If the tree is empty, set the root to a new node.

Step 4: If the tree is not empty, check whether a value of new node is smaller or larger than the node (here it is a root node).

Step 5: If a new node is smaller than or equal to the node, move to its left child.

Step 6: If a new node is larger than the node, move to its right child.

Step 7: Repeat the process until we reach to a leaf node.

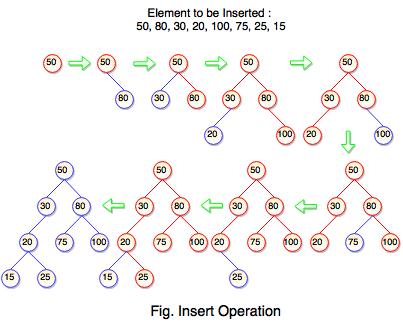
insert operation

The above tree is constructed a binary search tree by inserting the above elements {50, 80, 30, 20, 100, 75, 25, 15}. The diagram represents how the sequence of numbers or elements are inserted into a binary search tree.

2. Search Operation

Search operation is performed with O(log n) time complexity in a binary search tree.
This operation starts from the root node. It is used whenever an element is to be searched.

The following algorithm shows the search operation in binary search tree:

Step 1: Read the element from the user .

Step 2: Compare this element with the value of root node in a tree.

Step 3: If element and value are matching, display "Node is Found" and terminate the function.

Step 4: If element and value are not matching, check whether an element is smaller or larger than a node value.

Step 5: If an element is smaller, continue the search operation in left subtree.

Step 6: If an element is larger, continue the search operation in right subtree.

Step 7: Repeat the same process until we found the exact element.

Step 8: If an element with search value is found, display "Element is found" and terminate the function.

Step 9: If we reach to a leaf node and the search value is not match to a leaf node, display "Element is not found" and terminate the function.

Binary Tree Traversal

Binary tree traversing is a process of accessing every node of the tree and exactly once. A tree is defined in a recursive manner. Binary tree traversal also defined recursively.

There are three techniques of traversal:

1. Preorder Traversal
2. Postorder Traversal
3. Inorder Traversal

1. Preorder Traversal

Algorithm for preorder traversal

Step 1 : Start from the Root.

Step 2 : Then, go to the Left Subtree.

Step 3 : Then, go to the Right Subtree.

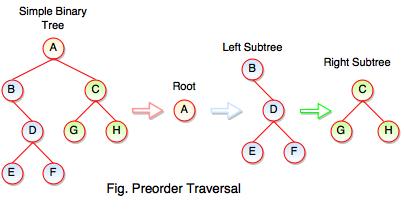
The above figure represents how preorder traversal actually works.

Following steps can be defined the flow of preorder traversal:

Step 1 : A + B (B + Preorder on D (D + Preorder on E and F)) + C (C + Preorder on G and H)

Step 2 : A + B + D (E + F) + C (G + H)

Step 3 : A + B + D + E + F + C + G + H

Preorder Traversal : A B C D E F G H

2. Postorder Traversal

Algorithm for postorder traversal

Step 1 : Start from the Left Subtree (Last Leaf).

Step 2 : Then, go to the Right Subtree.

Step 3 : Then, go to the Root.

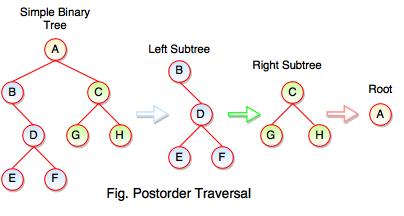
The above figure represents how postorder traversal actually works.

Following steps can be defined the flow of postorder traversal:

Step 1 : As we know, preorder traversal starts from left subtree (last leaf) ((Postorder on E + Postorder on F) + D + B )) + ((Postorder on G + Postorder on H) + C) + (Root A)

Step 2 : (E + F) + D + B + (G + H) + C + A

Step 3 : E + F + D + B + G + H + C + A

Postorder Traversal : E F D B G H C A

3. Inorder Traversal

Algorithm for inorder traversal

Step 1 : Start from the Left Subtree.

Step 2 : Then, visit the Root.

Step 3 : Then, go to the Right Subtree.

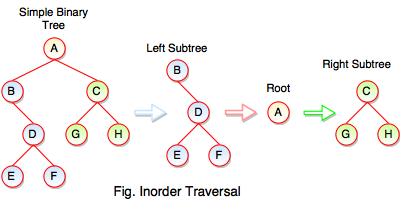
The above figure represents how inorder traversal actually works.

Following steps can be defined the flow of inorder traversal:

Step 1 : B + (Inorder on E) + D + (Inorder on F) + (Root A ) + (Inorder on G) + C (Inorder on H)

Step 2 : B + (E) + D + (F) + A + G + C + H

Step 3 : B + E + D + F + A + G + C + H

Inorder Traversal : B E D F A G C H

Example: Program for Binary Tree

#include<stdio.h>
#include<stdlib.h>

struct node
{
      int data;
      struct node *rlink;
      struct node *llink;
}*tmp=NULL;

typedef struct node NODE;
NODE *create();
void preorder(NODE *);
void inorder(NODE *);
void postorder(NODE *);
void insert(NODE *);

int main()
{
     int n,i,ch;
     do
     {
          printf("\n\n1.Create\n\n2.Insert\n\n3.Preorder\n\n4.Postorder\n\n5.Inorder\n\n6.Exit\n\n");
          printf("\n\nEnter Your Choice : ");
          scanf("%d",&ch);
          switch(ch)
          {
               case 1:
                    tmp=create();
                    break;
               case 2:
                    insert(tmp);
                    break;
               case 3:
                    printf("\n\nDisplay Tree in Preorder Traversal : ");
                    preorder(tmp);
                    break;
               case 4:
                    printf("\n\nDisplay Tree in Postorder Traversal : ");
                    postorder(tmp);
                    break;
               case 5:
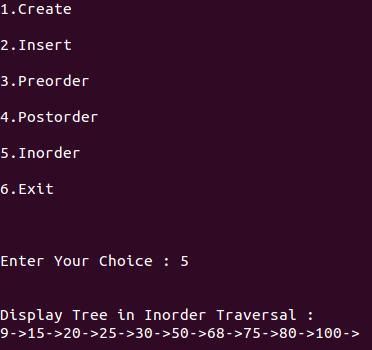
                    printf("\n\nDisplay Tree in Inorder Traversal : ");
                    inorder(tmp);
                    break;
               case 6:
                    exit(0);
                    default:
                    printf("\n Inavild Choice..");
          }
     }
     while(n!=5);
}
void insert(NODE *root)
{
     NODE *newnode;
     if(root==NULL)
     {
          newnode=create();
          root=newnode;
     }
     else
     {
          newnode=create();
          while(1)
          {
               if(newnode->data<root->data)
               {
                    if(root->llink==NULL)
                    {
                         root->llink=newnode;
                         break;
                    }
                    root=root->llink;
               }
               if(newnode->data>root->data)
               {
                    if(root->rlink==NULL)
                    {
                         root->rlink=newnode;
                         break;
                    }
                    root=root->rlink;
               }
          }
     }
}
NODE *create()
{
     NODE *newnode;
     int n;
     newnode=(NODE *)malloc(sizeof(NODE));
     printf("\n\nEnter the Data ");
     scanf("%d",&n);
     newnode->data=n;
     newnode->llink=NULL;
     newnode->rlink=NULL;
     return(newnode);
}
void postorder(NODE *tmp)
{
     if(tmp!=NULL)
     {
          postorder(tmp->llink);
          postorder(tmp->rlink);
          printf("%d->",tmp->data);
     }
}
void inorder(NODE *tmp)
{
     if(tmp!=NULL)
     {
          inorder(tmp->llink);
          printf("%d->",tmp->data);
          inorder(tmp->rlink);
     }
}
void preorder(NODE *tmp)
{
     if(tmp!=NULL)
     {
          printf("%d->",tmp->data);
          preorder(tmp->llink);
          preorder(tmp->rlink);
     }
}