What is Graph?
- Graph is an abstract data type.
- It is a pictorial representation of a set of objects where some pairs of objects are connected by links.
- Graph is used to implement the undirected graph and directed graph concepts from mathematics.
- It represents many real life application. Graphs are used to represent the networks. Network includes path in a city, telephone network etc.
- It is used in social networks like Facebook, LinkedIn etc.
Graph consists of two following components:
1. Vertices
2. Edges- Graph is a set of vertices (V) and set of edges (E).
- V is a finite number of vertices also called as nodes.
- E is a set of ordered pair of vertices representing edges.
- For example, in Facebook, each person is represented with a vertex or a node. Each node is a structure and contains the information like user id, user name, gender etc.
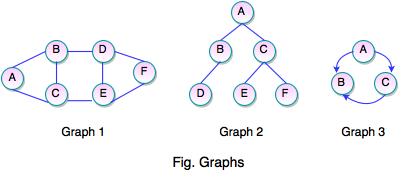
- The above figures represent the graphs. The set representation for each of these graphs are as follows:
Graph 1:
V = {A, B, C, D, E, F}
E = {(A, B), (A, C), (B, C), (B, D), (D, E), (D, F), (E, F)}
Graph 2:
V = {A, B, C, D, E, F}
E = {(A, B), (A, C), (B, D), (C, E), (C, F)}
Graph 3:
V = {A, B, C}
E = {(A, B), (A, C), (C, B)}
Directed Graph
- If a graph contains ordered pair of vertices, is said to be a Directed Graph.
- If an edge is represented using a pair of vertices (V1, V2), the edge is said to be directed from V1 to V2.
- The first element of the pair V1 is called the start vertex and the second element of the pair V2 is called the end vertex.
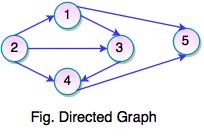
Set of Vertices V = {1, 2, 3, 4, 5, 5}
Set of Edges W = {(1, 3), (1, 5), (2, 1), (2, 3), (2, 4), (3, 4), (4, 5)}
Undirected Graph
- If a graph contains unordered pair of vertices, is said to be an Undirected Graph.
- In this graph, pair of vertices represents the same edge.
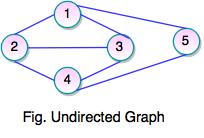
Set of Vertices V = {1, 2, 3, 4, 5}
Set of Edges E = {(1, 2), (1, 3), (1, 5), (2, 1), (2, 3), (2, 4), (3, 4), (4, 5)}- In an undirected graph, the nodes are connected by undirected arcs.
- It is an edge that has no arrow. Both the ends of an undirected arc are equivalent, there is no head or tail.
Representation of Graphs
Adjacency Matrix
- Adjacency matrix is a way to represent a graph.
- It shows which nodes are adjacent to one another.
- Graph is represented using a square matrix.
- Graph can be divided into two categories:
a. Sparse Graph
b. Dense Graph
a. Sparse graph contains less number of edges.
b. Dense graph contains number of edges as compared to sparse graph.
- Adjacency matrix is best for dense graph, but for sparse graph, it is not required.
- Adjacency matrix is good solution for dense graph which implies having constant number of vertices.
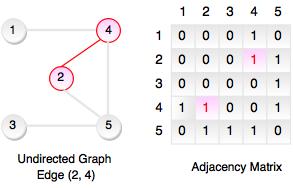
- Adjacency matrix of an undirected graph is always a symmetric matrix which means an edge (i, j) implies the edge (j, i).
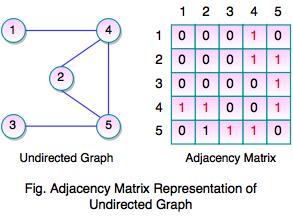
- The above graph represents undirected graph with the adjacency matrix representation. It shows adjacency matrix of undirected graph is symmetric. If there is an edge (2, 4), there is also an edge (4, 2).
- Adjacency matrix of a directed graph is never symmetric adj[i][j] = 1, indicated a directed edge from vertex i to vertex j.
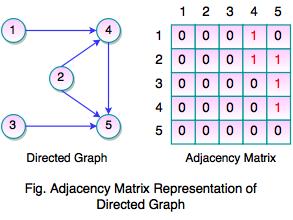
- The above graph represents directed graph with the adjacency matrix representation. It shows adjacency matrix of directed graph which is never symmetric. If there is an edge (2, 4), there is not an edge (4, 2). It indicates direct edge from vertex i to vertex j.
Advantages of Adjacency Matrix- Adjacency matrix representation of graph is very simple to implement.
- Adding or removing time of an edge can be done in O(1) time. Same time is required to check, if there is an edge between two vertices.
- It is very convenient and simple to program.
Disadvantages of Adjacency Matrix- It consumes huge amount of memory for storing big graphs.
- It requires huge efforts for adding or removing a vertex. If you are constructing a graph in dynamic structure, adjacency matrix is quite slow for big graphs.
Adjacency List
- Adjacency list is another representation of graphs.
- It is a collection of unordered list, used to represent a finite graphs.
- Each list describes the set of neighbors of a vertex in the graph.
- Adjacency list requires less amount of memory.
- For every vertex, adjacency list stores a list of vertices, which are adjacent to the current one.
- In adjacency list, an array of linked list is used. Size of the array is equal to the number of vertices.
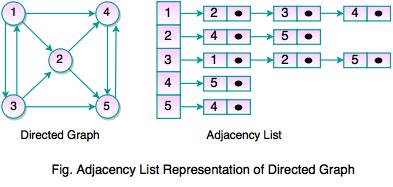
- In adjacency list, an entry array[i] represents the linked list of vertices adjacent to the ith vertex.
- Adjacency list allows to store the graph in more compact form than adjacency matrix.
- It allows to get the list of adjacent vertices in O(1) time.
Disadvantages of Adjacency List- It is not easy for adding or removing an edge to/from adjacent list.
- It does not allow to make an efficient implementation, if dynamically change of vertices number is required.
Important Note:
Vertex: Each node of the graph is represented as a vertex.
Edge: It represents a path between two vertices or a line between two vertices.
Path: It represents a sequence of edges between the two vertices.
Adjacency: If two nodes or vertices are connected to each other through an edge, it is said to be an adjacency.
Graph Traversal
- Graph traversal is a process of checking or updating each vertex in a graph.
- It is also known as Graph Search.
- Graph traversal means visiting each and exactly one node.
- Tree traversal is a special case of graph traversal.
There are two techniques used in graph traversal:
1. Depth First Search
2. Breadth First Search
1. Depth First Search
- Depth first search (DFS) is used for traversing a finite graph.
- DFS traverses the depth of any particular path before exploring its breadth.
- It explores one subtree before returning to the current node and then exploring the other subtree.
- DFS uses stack instead of queue.
- It traverses a graph in a depth-ward motion and gets the next vertex to start a search when a dead end occurs in any iteration.
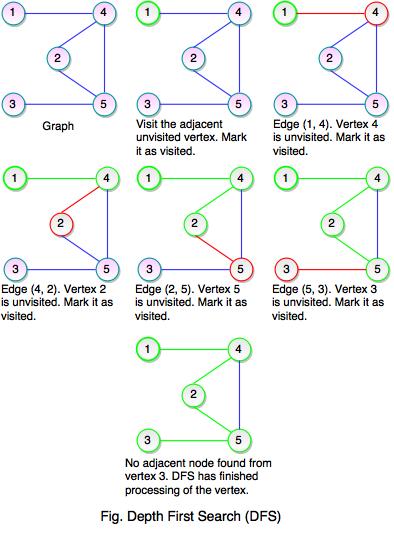
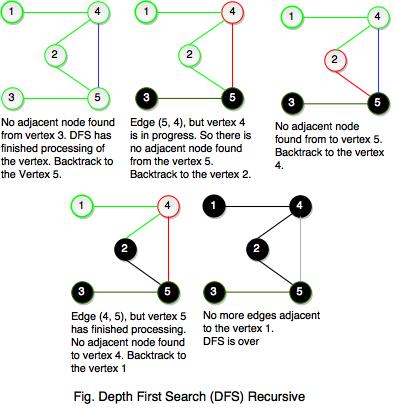
- As you see both the figures, DFS does not go though all the edges. The tree contains all the vertices of the graph if it is connected to the nodes and is called as Graph Spanning Tree. Graph spanning tree is exactly corresponds to the recursive calls of DFS.
- If a graph is disconnected then DFS will not be able to visit all of its vertices.
- DFS will pop up all the vertices from the stack which do not have adjacent nodes. The process is going on until we find a node that has unvisited adjacent node and if there is no more adjacent node, DFS is over.
2. Breadth First Search
- Breadth first search is used for traversing a finite graph.
- It visits the neighbor vertices before visiting the child vertices.
- BFS uses a queue for search process and gets the next vertex to start a search when a dead end occurs in any iteration.
- It traverses a graph in a breadth-ward motion.
- It is used to find the shortest path from one vertex to another.
- The main purpose of BFS is to traverse the graph as close as possible to the root node.
- BFS is a different approach for traversing the graph nodes.








