Types of Binary Tree

A tree is said to be binary tree when,

1. A binary tree has a root node. It may not have any child nodes(0 child nodes, NULL tree).

2. A root node may have one or two child nodes. Each node forms a binary tree itself.

3. The number of child nodes cannot be more than two.

4. It has a unique path from the root to every other node.

There are four types of binary tree:

1. Full Binary Tree
2. Complete Binary Tree
3. Skewed Binary Tree
4. Extended Binary Tree

1. Full Binary Tree

  • If each node of binary tree has either two children or no child at all, is said to be a Full Binary Tree.
  • Full binary tree is also called as Strictly Binary Tree.

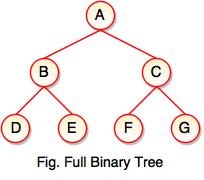
    • full binary tree
  • Every node in the tree has either 0 or 2 children.
  • Full binary tree is used to represent mathematical expressions.

2. Complete Binary Tree

  • If all levels of tree are completely filled except the last level and the last level has all keys as left as possible, is said to be a Complete Binary Tree.
  • Complete binary tree is also called as Perfect Binary Tree.

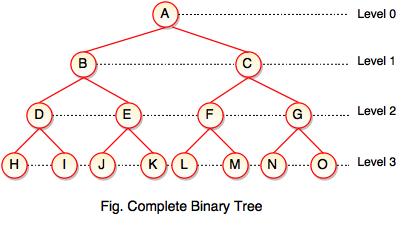
    • complete binary tree
  • In a complete binary tree, every internal node has exactly two children and all leaf nodes are at same level.
  • For example, at Level 2, there must be 22 = 4 nodes and at Level 3 there must be 23 = 8 nodes.

3. Skewed Binary Tree

  • If a tree which is dominated by left child node or right child node, is said to be a Skewed Binary Tree.
  • In a skewed binary tree, all nodes except one have only one child node. The remaining node has no child.

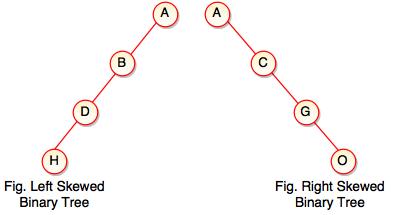
    • skewed binary tree
  • In a left skewed tree, most of the nodes have the left child without corresponding right child.
  • In a right skewed  tree, most of the nodes have the right child without corresponding left child.

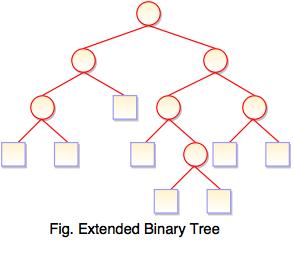
4. Extended Binary Tree

  • Extended binary tree consists of replacing every null subtree of the original tree with special nodes.
  • Empty circle represents internal node and filled circle represents external node.
  • The nodes from the original tree are internal nodes and the special nodes are external nodes.
  • Every internal node in the extended binary tree has exactly two children and every external node is a leaf. It displays the result which is a complete binary tree.
extended binary tree

AVL Tree

  • AVL tree is a height balanced tree.
  • It is a self-balancing binary search tree.
  • AVL tree is another balanced binary search tree.
  • It was invented by Adelson-Velskii and Landis.
  • AVL trees have a faster retrieval.
  • It takes O(logn) time for addition and deletion operation.
  • In AVL tree, heights of left and right subtree cannot be more than one for all nodes.

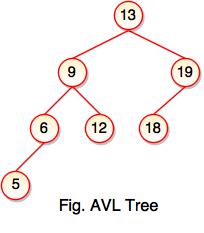
    • avl tree
  • The above tree is AVL tree because the difference between heights of left and right subtrees for every node is less than or equal to 1.

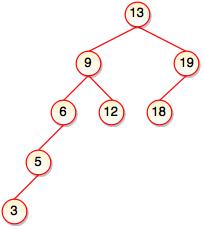
    • avl tree not

  • The above tree is not AVL because the difference between heights of left and right subtrees for 9 and 19 is greater than 1.
  • It checks the height of the left and right subtree and assures that the difference is not more than 1. The difference is called balance factor.
▲