Percentage - Aptitude Questions and Answers Part 3

11. Two candidates contested an election. The losing candidate got 40% votes and lost by 2000 votes. Find the total number of votes cast.

a. 5000
b. 8000
c. 10000
d. 20000

Answer: c. 10000

Explanation:

Total votes = a.
This means that, Votes of candidate 1 + Votes of candidate 2 = a

We know that, Votes of candidate 1 = 40% of a =40a
100
Hence, Votes of candidate 2 = (100% - 40%) of a = 60% of a =60a
100
1st candidate lost by 1000 votes = difference of votes between both candidates
∴60a-40a= 2000
100100
∴ a = 10,000.


12. Present population of a city is 60,000. It increases at the rate of 10%. Find the population of the city after 4 years.

a. 65,550
b. 80,500
c. 87,846
d. 88,550

Answer: c. 87,846

Explanation:

Tip:
Remember this formula. It is similar to formula for COMPOUND INTEREST.
Population after n years = P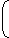1 ±R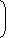n
100
P = Population; R = Rate of increase or decrease; n = number of years;
'+' = during increase; '-' = during decrease


Using formula given above -
Population after 4 years = 60,000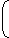1 +10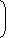4
100
=60,000 x 11 x 11 x 11 x 11= 87,846
10 x 10 x 10 x 10


13. Ram grew up in a small city with population 40,000 in 1982. He remembers that the census at the end of 1983 said that the population has increased by 25% but due to an epidemic, the population fell down by 30% in 1984. In 1985 there was an increase of 40% in the population. Find the population of the city at the end of 1985.   

a. 70250
b. 72250
c. 76550
d. 73500

Answer: d. 73500

Explanation:

Tip:
Remember this formula. It is similar to formula for COMPOUND INTEREST.
Population after n years = P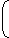1 ±R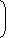n
100
P = Population; R = Rate of increase or decrease; n = number of years;
'+' = during increase; '-' = during decrease


Using formula given above -
Rate 1 = R1 = 25% (increase);
Rate 2 = R2 = 30% (decrease);
Rate 3 = R3 = 40% (increase)
Population after 3 years = 60,0001 +25 1 -301 +40
100100100
= 60,00012570140
100100100
= 73,500


14. A Principal wanted to improve the performance of her school in languages and asks for annual report from teachers, Filing the annual report for Class V, a teacher commented, 15% of students failed in English, 25% of students failed in Hindi while 10% of students failed in both the subjects. What percentage of students passed in both the subjects English and Hindi?

a. 60%
b. 70%
c. 80%
d. 90%

Answer: b. 70%

Explanation:

Usual Mistake: Percentage of Students failing in both subjects = 25% + 15% = 40%
But as shown in the below diagram, the students who failed both subjects (10%) are counted twice - Once in 15% (blue circle) and once again in 25% (orange circle).



We need to subtract this double counting.
So students who failed subjects would be = 25% + 15% - 10% = 30%

Remember:
Subtract only once, not twice!


Percentage of students who passed in both subjects = (100 - 30) % = 70%
Thus, 70% passed in both subjects.


15. The monthly finance tracker of a person reads as below

ItemExpenses out of income
Food30%
House Rent35%
Travel9%
Education17%

Savings for the month : Rs 7200/-

Find the amount he spent on travel that month.

a. Rs. 7000
b. Rs. 7100
c. Rs. 7200
d. Rs. 7300

Answer: c. Rs. 7200

▲