Permutation and Combination - Aptitude Questions and Answers Part 2

6. A television show was attended by 12 well known celebrities. Each one of them shook hands with each other once at the beginning of the show. Find the number of handshakes that took place on the show.  

a. 24
b. 66
c. 120
d. 132

Answer: b. 66

Explanation:

There are 12 celebrities. A handshake needs 2 people.
This simply means in how many ways 2 people can be selected out of 12.
So the answer is 12C2

nCr =n!
r!(n-r)!
∴ 12C2 =12!=12 x 11= 66 = Number of handshakes
2!(12-2)!2

Tip:
If there are n people and they shake hands only once with each other, then,
Number of handshakes = nC2 =n(n-1)
2


7. Electricity department needs to generate bills for a locality. They decide the bill no. to be a 6 digit number with 4 and 7 fixed as first and last digits. No digits should be repeated anywhere in the bill number. 4 denotes station number and 7 denotes the area. How many such bill numbers can the electricity department generate?

a. 890
b. 1680
c. 5040
d. 10080

Answer: b. 1680

Explanation:

We need 6 digits

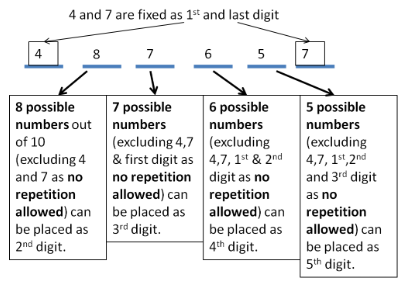
permutation and combination

So total numbers possible = 8 x 7 x 6 x 5 = 56 x 30 = 1680


8. A cricket group of 6 members is to be formed from Academy A. The members of the group are to be from 3 bowlers, 4 batsman and 5 coaches. How many ways are possible to form the group so that it has either 3 coaches and 3 batsman or 2 bowlers and 4 coaches.

a. 27
b. 55
c. 90
d. 144

Answer: b. 55

Explanation:

We need to SELECT people.

Tip:
SELECT = Combination = nCr =n!
r!(n-r)!
SELECT and ARRANGE = Permutation = nPr =n!
(n-r)!
Also ,  AND = MULTIPLY ; OR = ADD


3 coaches and 3 batsman or 2 bowlers and 4 coaches means
(3 coaches x 3 batsman) + (2 bowlers x 4 coaches)
Select 3 coaches out of 5 = 5C3 =5!= 10
3!2!
Select 3 batsman out of 4 = 4C3 =4!= 4
3!1!
Select 2 bowlers out of 3 = 3C2 =3!= 3
2!1!
Select 4 coaches out of 5 = 5C4 =5!= 5
4!1!
Total ways to form the group = (10 x 4) + (3 x 5) = 40 + 15 = 55


9. There are 20 stops for the local trains running between Churchgate and Virar. A passenger travelling between any two stops needs to buy a ticket. How many types of tickets are required to be made to meet all the possibilities?

a. 72
b. 190
c. 380
d. 760

Answer: c. 380

Explanation:

There are 20 stations. Ticket is needed between 2 stops.
That means, we simply need to select 2 stops from possible 20 stops.

Tip:
SELECT = Combination = nCr =n!
r!(n-r)!
SELECT and ARRANGE = Permutation = nPr =n!
(n-r)!

That can be done by 20C2 ways =20!=20!= 190 ways
2!(20-2)!2!18!
This is when we start from one side.
When we travel from the other side we will need separate ticket.
That means while going from A to B and B to A, we will need separate tickets.
So again from other side we need 190 tickets.
Total tickets = 380 tickets


10. 19 ladies are there in a group. Find the number of ways, in which they can be made to stand in 2 circles of 9 and 10 ladies?

a. 9! X 8!
b. 19C10 x 9! X 8!
c. 19C9 x 9! X 10!
d. None of the above

Answer: b. 19C10 x 9! X 8!

Explanation:

Here, we first have to select 10 ladies from 19.

Tip:
SELECT = Combination = nCr =n!
r!(n-r)!
SELECT and ARRANGE = Permutation = nPr =n!
(n-r)!


Select = Combination
∴ Select 10 ladies = 19C10

Tip:
We can arrange 'n' things in 'n!' ways.
But if they are to be arranged in a circle,
then we can arrange them in (n-1)! ways.


Arrange 10 ladies in circle = 10 - 1 = 9! ways
19 - 10 = 9 ladies remain.
Arrange remaining 9 ladies in another circle = 9 - 1 = 8! ways
∴ Total ways to arrange 19 ladies in 2 required circles = 19C10 x 9! X 8!

▲