a. 99
b. 132
c. 144
d. 169
Answer: c. 144
Explanation:
Let 1st number be X.
| ∴ 2nd number = | X | and 3rd number = | X |
| 4 | 5 |
| Average = | X + X/4 + X/5 | = 87 |
| 3 |
| ∴ | 29X | = 87 |
| 20 * 3 |
The smallest number is 3rd number.
∴ 1st - 3rd number = 180 - (180/5) = 144
7. Prithvi has 2 boxes. There are some coins in each of these boxes. If 20 coins from second box are shifted to first box then, the number of coins in each box get interchanged. But if 10 coins from first box are put into second box, then number of coins in second box become twice the number in first one. How many pebbles do the two boxes have each?
a. 60 and 40
b. 50 and 70
c. 70 and 90
d. 80 and 100
Answer: b. 50 and 70
Explanation:
We see that, all the options satisfy the first given condition of interchanging number of coins. Now, let's check for the second condition.
Option 1 → 60 - 10 = 50 and 40 + 10 = 50 ∴ 2nd condition not satisfied
Option 2 → 80 - 10 = 70 and 100 + 10 = 110 ∴ 2nd condition not satisfied
Option 3 → 70 - 10 = 60 and 90 + 10 = 100 ∴ 2nd condition not satisfied
Option 4 → No need to calculate. Directly mark this as other 3 are wrong.
But if you wish you can check.
50 - 10 = 40 and 70 + 10 = 80
80 = 2 times 40 ∴ 2nd condition satisfied
8. When Radha tries to exchange the digit's in unit's and ten's place of a number, she finds that the difference between the original and newly formed number is 27. She also notices that the unit's place digit is twice the one on hundred's place. While, the digit in ten's place is thrice that of the one in hundred's place. What is the ¾ of original number?
a. 99
b. 297
c. 369
d. 396
Answer: b. 297
Explanation:
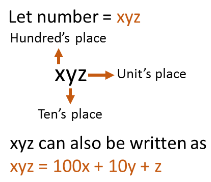
Here let digit in hundred's place be H
∴ In Unit's place we have 2H and Ten's place we have 3H
∴ Original number = 100H + 10 (3H) + 2H = 132H
If we exchange unit's and ten's digits, we get
New Number = 100H + 10 (2H) + 3H = 123H
Also, 132H - 123H = 27
∴ H = 3
Original Number = 132H = 396
¾ of 396 = 297
9. Raman subtracts two numbers and finds the square of the resultant to be 9. When he squares the two numbers and adds them. The resultant is 225. Find the product of two numbers.
a. 96
b. 108
c. 125
d. 169
Answer: b. 108
Explanation:
Let numbers be A and B
∴ (A - B)2 = 9
∴ A2 - 2AB + B2 = 9
Further, A2 + B2 = 225
∴ 225 - 2AB = 9
∴ AB = 108 = product of the two numbers
Going further if the question asks you to find out the values of two numbers
Consider equation (A+B)2 = A2 + 2AB + B2
∴ (A+B)2 = 225 + 2 x 108 = 441
A + B = 21 ---------- (1)
We know, (A - B)2 = 9
∴ A - B = 3 ---------- (2)
Adding (1) and (2) we get, 2A = 24
∴ A = 12
Put the value of A in equation 2. We get B = 9
10. In a school 2% children have 5 books each. But 8% are carrying no books at all. Out of the remaining children 18% have 4 books and 27% have only one book. How many children are there in the school, if 297 children are carrying either 2 or 3 books each?
a. 550
b. 600
c. 725
d. 850
Answer: b. 600
Explanation:
Let there be 100 children.
8% have 0 books and 2 % have 5 books.
So, that makes 10% = 10 children
Remaining are 100 - 10 = 90 children
Of these 90, 27% have one book and 18% have 4 books each.
So that is 27 + 18 = 45% out of 90
So remaining children (100 - 45%) = 55% out of 90 = have 2 or 3 books
| ∴ Remaining children = | 55 | x 90 = 49.5 children |
| 100 |
For ? children : 297 children have 2 or 3 books
| ∴ ? = | 297 x 100 | = 600 children are there in the school. |
| 49.5 |
