Heap Sort
- Heap sort is a comparison based sorting algorithm.
- It is a special tree-based data structure.
- Heap sort is similar to selection sort. The only difference is, it finds largest element and places the it at the end.
- This sort is not a stable sort. It requires a constant space for sorting a list.
- It is very fast and widely used for sorting.
1. Shape Property
2. Heap Property
1. Shape property represents all the nodes or levels of the tree are fully filled. Heap data structure is a complete binary tree.
2. Heap property is a binary tree with special characteristics. It can be classified into two types:
I. Max-Heap
II. Min Heap
I. Max Heap: If the parent nodes are greater than their child nodes, it is called a Max-Heap.
II. Min Heap: If the parent nodes are smaller than their child nodes, it is called a Min-Heap.
Example: Program for Heap Sort
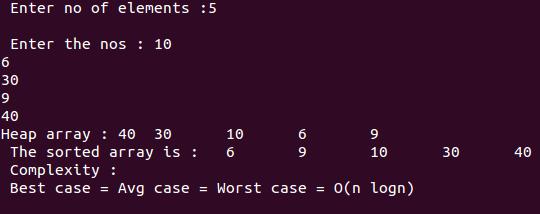
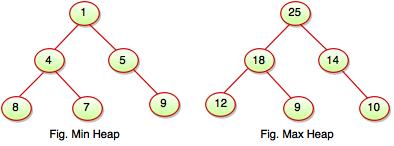
#include <stdio.h>
void main()
{
int heap[10], no, i, j, c, root, temp;
printf("\n Enter no of elements :");
scanf("%d", &no);
printf("\n Enter the nos : ");
for (i = 0; i < no; i++)
scanf("%d", &heap[i]);
for (i = 1; i < no; i++)
{
c = i;
do
{
root = (c - 1) / 2;
if (heap[root] < heap[c]) /* to create MAX heap array */
{
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
c = root;
} while (c != 0);
}
printf("Heap array : ");
for (i = 0; i < no; i++)
printf("%d\t ", heap[i]);
for (j = no - 1; j >= 0; j--)
{
temp = heap[0];
heap[0] = heap[j]; /* swap max element with rightmost leaf element */
heap[j] = temp;
root = 0;
do
{
c = 2 * root + 1; /* left node of root element */
if ((heap[c] < heap[c + 1]) && c < j-1)
c++;
if (heap[root]<heap[c] && c<j) /* again rearrange to max heap array */
{
temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c;
} while (c < j);
}
printf("\n The sorted array is : ");
for (i = 0; i < no; i++)
printf("\t %d", heap[i]);
printf("\n Complexity : \n Best case = Avg case = Worst case = O(n logn) \n");
}
Output:
